پایتون: تابع خطا (Error Function) و کاربرد آن در چاه‌آزمایی

تابع خطا (Error Function) در ریاضیات، تابعی غیراصلی (نداشتن ضابطه صریح) است که در علوم احتمالات، مواد، آمار و معادلات دیفرانسیل با مشتقات جزئی استفاده می‌شود. تعریف این تابع به صورت زیر است (منبع: ویکی پدیا):

همچنین متمم تابع خطا (Complementary Error Function) نیز به شکل زیر تعریف می‌شود:

نمودار تابع خطا

جدول تابع خطا

علاوه بر اینها، در زبان برنامه‌نویسی پایتون نیز دستوری وجود دارد که می‌توان تابع خطای هر مقداری را محسابه نمود:

from math import *

erf (2)

>> 0.9953222650189527

erfc (2)

>> 0.004677734981047268

یکی از کاربردهای تابع خطا در درس چاه‌آزمایی می‌باشد. مثلاً گرینگارتن و همکاران با استفاده از توابع گرین (Green’s function)، معادله انتشار را برای یک چاه شکافدار (مدل شار یکنواخت) حل نمودند و به رابطه زیر رسیدند:

همان‌طور که مشاهده می‌کنید برای محاسبه فشار بی‌بعد در این رابطه، باید مقادیر تابع خطا را داشته باشیم. 

دانلود جدول تابع خطا و متمم تابع خطا

مدلسازی محاسباتی (Computational Modelling) چیست؟

اولین مرحله در مطالعه یک فرایند با شبیه‌سازی کامپیوتری، توسعه یک مدل برای سیستم واقعی است.

هنگام مطالعه حرکت یک شیء کوچک که تحت تأثیر نیروی گرانش زمین قرار دارد، ما ممکن است که بتوانیم نیروی اصطکاک هوا را نادیده بگیریم. در این حالت، مدل ما یک تقریبی از سیستم واقعی خواهد بود. معمولاً این مدل این اجازه را به ما خواهد داد تا رفتار سیستم (به فرم تقریبی) را از طریق معادلات ریاضی بیان کنیم، که اغلب شامل معادلات دیفرانسیل معمولی (ODE) یا معادلات دیفرانسیل با مشتقات جزئی (PDE) هستند.

در علوم طبیعی مانند فیزیک، شیمی و مهندسی، اغلب سخت نیست که یک مدل مناسب پیدا کنیم، اگرچه معادلات حاصل شده برای حل بسیار مشکل هستند و در اکثر موارد نمی‌توان آن‌ها را به طور تحلیلی حل نمود.

از سوی دیگر، در مواردی که نمی‌توان آن‌ها را به خوبی در چارچوب ریاضیات شرح داد و به رفتار اشیائی وابسته هستند که اقدام آن‌ها را نمی‌توان به طور قطعی پیش‌بینی نمود (مانند انسان‌ها)، یافتن یک مدل خوب برای توصیف واقعیت بسیار مشکل است. به عنوان یک قاعده کلی، در این رشته‌ها معادلات حاصله را ساده‌تر می‌توان حل نمود، اما یافتن آن‌ها سخت‌تر است و اعتبار یک مدل باید بیشتر مورد سوال قرار بگیرد. برخی از مثال‌های معمول عبارتند از تلاش برای شبیه‌سازی اقتصاد، استفاده از منابع طبیعی و غیره.

تا کنون، ما فقط در مورد توسعه مدل‌ها برای توصیف واقعیت بحث کرده‌ایم، و استفاده از این مدل‌ها لزوماً شامل کامپیوتر یا کار عددی نیست. در حقیقت، اگر معادله یک مدل بتواند به صورت تحلیلی حل شود، باید این کار را انجام داد و راه حل معادله را نوشت.

در عمل، تقریباً هیچ معادله مدل یک سیستم مورد نظر را نمی‌توان به صورت تحلیلی حل کرد، و این جایی است که کامپیوتر وارد می‌شود: با استفاده از روش‌های عددی، ما حداقل می‌توانیم مدل را برای یک مجموعه خاص از شرایط مرزی مطالعه کنیم.

به طور واضح مطلوب است که راه‌های تحلیلی را در هر کجا که امکان‌پذیر است پیدا کنید، اما تعداد مسائلی که این امکان وجود دارد کم هستند. معمولاً نتایج عددی یک شبیه‌سازی کامپیوتری بسیار مفید است (با وجود کاستی‌های نتایج عددی در مقایسه با روش تحلیلی)، زیرا این تنها راه ممکن برای مطالعه سیستم است.

نام مدلسازی کامپیوتری از دو مرحله برگرفته شده است: 1) مدلسازی؛ یعنی پیدا کردن توصیف مدل یک سیستم واقعی و 2) حل معادلات مربوط به مدل با استفاده از روش‌های محاسباتی، زیرا این تنها راه حل معادلات می‌باشد.

تعدادی زیادی پکیج وجود دارند که قابلیت‌های مدلسازی محاسباتی را ارائه می‌دهند. اگر این‌ها نیازهای تحقیق یا طراحی را برآورده کنند، و هرگونه پردازش و به تصویر کشیدن داده‌ها از طریق ابزارهای موجود پشتیبانی شود، می‌توان مطالعات مدلسازی محاسباتی را بدون هیچ گونه دانش برنامه‌نویسی عمیق‌تر انجام داد.

در یک محیط تحقیقاتی – هم در دانشگاه و هم در صنعت – اغلب به نقطه‌ای می‌رسند که پکیج‌های موجود قادر به انجام شبیه‌سازی مورد نظر نمی‌باشند. در این حالت، مهارت‌های برنامه‌نویسی مورد نیاز است.

درک نحوه ایجاد یک شبیه‌سازی کامپیوتری تقریباً به این صورت است: 1) یافتن مدل (اغلب به معنای یافتن معادلات درست می‌باشد)؛ 2) دانستن اینکه چگونه این معادلات را به صورت عددی حل کنیم؛ 3) پیاده‌سازی روش‌هایی برای محاسبه این راه حل‌ها (این برنامه‌نویسی است).

 

 

پایتون: برازش منحنی (Curve Fitting)

یکی از موضوعات مهم ریاضیات و آمار که کاربرد زیادی در رشته‌های مهندسی دارد، مبحث برازش منحنی (Curve Fitting) می‌باشد. 

هدف ما در برازش منحنی آن است که بهترین خط یا منحنی ممکن را از داده‌های موجود عبور دهیم. برای آنکه متوجه شویم که بهترین چندجمله‌ای یا منحنی ممکن را انتخاب کرده‌ایم، باید مجموع مربعات باقمانده‌ها حداقل باشد:

.The most common choice is to minimize the sum of squared residuals

معرفی چند تابع:

1- z = polyfit (x, y, n) 

این تابع، مقادیر x داده و مقادیر y داده‌ها را دریافت می‌کند و سپس یک منحنی درجه n ام از داده‌ها عبور می‌دهد به نحوی که بهترین انطباق ممکن را داشته باشد (حداقل مربعات). 

2- p = poly1d (z)

یک تابع چند جمله‌ای از ضرایب می‌سازد.

بررسی یک مثال از مبحث برازش منحنی:

from numpy import *

x = array ([0.0 , 1.0 , 2.0 , 3.0 , 4.0 , 5.0])

y = array ([0.0 , 0.8 , 0.9 , 0.1 , -0.8 , -1.0])

z = polyfit (x, y, 3)

p = poly1d (z)

xs = [ 0.1 * i for i in range (50)]

ys = [p ( x ) for x in xs]

from pylab import *

plot (x, y, 'o', label='data')

plot (xs, ys, label='fitted curve')

ylabel ('y')

xlabel ('x')

show ()

پایتون: نحوه محاسبه Exponential Integral در چاه‌آزمایی

الآن در حال حل یکی از مثال‌های کتاب چاه‌آزمایی جان لی بودم که در میان مسیر باید مقدار Exponential Integral را محاسبه می‌کردم. روش معمول آن است که به جداول خود کتاب مراجعه کنیم و با کمی جستجو مقدار آن را بدست آوریم. ولی راه حل بهتر آن است که این کار را با استفاده از اکسل، پایتون، متلب و غیره انجام دهیم تا هم سریع‌تر باشد و هم مقدار دقیق‌تری بدست آید. 

ماژول Scipy یک تابع مناسبی برای محاسبه مقادیر Ei ارائه می‌دهد:

from scipy import*

x=expi(-0.5)

print(x)

نتیجه:

x = - 0.559773594776

کانال سایت در تلگرام

پایتون: روش رانگ کاتا مرتبه سوم (Runge-Kutta 3rd Order)

در مسائل مقدار اولیه، مقدار تابع در نقطه شروع داده می‌شود و با استفاده از روش‌های موجود مقدار آن را در سایر نقاط بدست می‌آوریم. در این صورت منحنی تغییرات متغیر تابع بر حسب متغیر مستقل قابل رسم خواهد بود.

از جمله روش‌های حل مسائل مقدار اولیه می‌توان به روش‌های تیلور، اویلر و رانگ کاتا مرتبه دوم، سوم و چهارم اشاره نمود. در کلیه این روش‌ها مختصات هر نقطه با استفاده از مختصات نقطه ماقبلش بدست می‌آید. اساس کلیه این روش‌ها، استفاده از سری تیلور است.

تذکر: برای مطالعه توضیحات بیشتر به کتاب «کاربرد ریاضیات در مهندسی شیمی - روش‌های عددی» نوشته دکتر خراط مراجعه کنید.

خلاصه روش رانگ کاتا مرتبه سوم:

در اینجا قصد دارم به بررسی یک مثال به روش رانگ کاتا - 3 بپردازم. قبلاً این مثال را به روش‌های اویلر، رانگ کاتا-2 و رانگ کاتا-4 نیز حل کرده‌ام (+ و + و +)

مثال:

معادله دیفرانسیل زیر را با استفاده از روش رانگ کاتا مرتبه سوم و برای حالت h = 0.5 حل کنید و مقدار تابع را تا x = 3.5 محاسبه کنید.

حل با استفاده از زبان برنامه نویسی پایتون (کدنویسی در محیط Spyder):

import numpy as np

from matplotlib import pyplot as plt

x0=1

y0=1

xf=3.5

n=6

h=(xf-x0)/(n-1)

x=np.linspace(x0,xf,n)

y=np.zeros([n])

y[0]=y0

for i in range(1,n):

    k1=h*x[i-1]*y[i-1]**(1/3)

    k2=h*(x[i-1]+0.5*h)*(y[i-1]+0.5*k1)**(1/3)

    k3=h*(x[i-1]+h)*(y[i-1]+2*k2-k1)**(1/3)

    y[i]=y[i-1]+(1/6)*(k1+4*k2+k3)

for i in range(n):

    print(x[i],y[i])

plt.plot(x,y,'o')

plt.xlabel('value of x')

plt.ylabel('value of y')

plt.title('Approximate Solution with RK-3 Method')

plt.show()

نتایج:

1.0                          1.0

1.5           1.6855277908

2.0            2.826623146

2.5           4.5570242827

3.0           7.0160178606

3.5           10.345325211

کانال سایت در تلگرام

پایتون: روش رانگ کاتا مرتبه چهارم (Runge-Kutta 4th Order)

در مسائل مقدار اولیه، مقدار تابع در نقطه شروع داده می‌شود و با استفاده از روش‌های موجود مقدار آن را در سایر نقاط بدست می‌آوریم. در این صورت منحنی تغییرات متغیر تابع بر حسب متغیر مستقل قابل رسم خواهد بود.

از جمله روش‌های حل مسائل مقدار اولیه می‌توان به روش‌های تیلور، اویلر و رانگ کاتا مرتبه دوم، سوم و چهارم اشاره نمود. در کلیه این روش‌ها مختصات هر نقطه با استفاده از مختصات نقطه ماقبلش بدست می‌آید. اساس کلیه این روش‌ها، استفاده از سری تیلور است.

تذکر: برای مطالعه توضیحات بیشتر به کتاب «کاربرد ریاضیات در مهندسی شیمی - روش‌های عددی» نوشته دکتر خراط مراجعه کنید.

خلاصه روش رانگ کاتا مرتبه چهارم:

در اینجا قصد دارم به بررسی یک مثال به روش رانگ کاتا - 4 بپردازم. قبلاً این مثال را به روش‌های اویلر و رانگ کاتا-2 نیز حل کرده‌ام (+ و +)

مثال:

معادله دیفرانسیل زیر را با استفاده از روش رانگ کاتا مرتبه چهارم و برای حالت h = 0.5 حل کنید و مقدار تابع را تا x = 3.5 محاسبه کنید.

حل با استفاده از زبان برنامه نویسی پایتون (کدنویسی در محیط Spyder):

import numpy as np

from matplotlib import pyplot as plt

x0=1

y0=1

xf=3.5

n=6

h=(xf-x0)/(n-1)

x=np.linspace(x0,xf,n)

y=np.zeros([n])

y[0]=y0

for i in range(1,n):

    k1=h*x[i-1]*y[i-1]**(1/3)

    k2=h*(x[i-1]+0.5*h)*(y[i-1]+0.5*k1)**(1/3)

    k3=h*(x[i-1]+0.5*h)*(y[i-1]+0.5*k2)**(1/3)

    k4=h*(x[i-1]+h)*(y[i-1]+k3)**(1/3)

    y[i]=y[i-1]+(1/6)*(k1+2*k2+2*k3+k4)

for i in range(n):

    print(x[i],y[i])

plt.plot(x,y,'o')

plt.xlabel('value of x')

plt.ylabel('value of y')

plt.title('Approximate Solution with RK-4 Method')

plt.show()

نتایج:

1.0      1.0

1.5       1.6860902679

2.0     2.82824535285

2.5     4.56006327111

3.0     7.02071665246

3.5     10.3518481736

پایتون: روش رانگ کاتا مرتبه دوم (Runge-Kutta 2nd Order)

در مسائل مقدار اولیه، مقدار تابع در نقطه شروع داده می شود و با استفاده از روش های موجود مقدار آن را در سایر نقاط بدست می آوریم. در اینصورت منحنی تغییرات متغیر تابع بر حسب متغیر مستقل قابل رسم خواهد بود.

از جمله روش های حل مسائل مقدار اولیه می توان به روش های تیلور، اویلر و رانگ کاتا مرتبه دوم، سوم و چهارم اشاره نمود. در کلیه این روش ها مختصات هر نقطه با استفاده از مختصات نقطه ماقبلش بدست می آید. اساس کلیه این روش ها، استفاده از سری تیلور است.

تذکر: برای مطالعه توضیحات در مورد روش رانگ کاتا-2 به کتاب «کاربرد ریاضیات در مهندسی شیمی - روش های عددی» نوشته دکتر خراط مراجعه کنید.

خلاصه این روش:

در اینجا قصد دارم به بررسی یک مثال به روش رانگ کاتا - 2 بپردازم. قبلاً این مثال را به روش اویلر نیز حل کرده ام (این پست).

مثال:

معادله دیفرانسیل زیر را با استفاده از روش رانگ کاتا مرتبه دوم و برای حالت h = 0.5 حل کنید و مقدار تابع را تا x = 3.5 محاسبه کنید.

حل با استفاده از زبان برنامه نویسی پایتون (کدنویسی در محیط Spyder):

import numpy as np

from matplotlib import pyplot as plt

x0=1

y0=1

xf=3.5

n=6

h=(xf-x0)/(n-1)

x=np.linspace(x0,xf,n)

y=np.zeros([n])

y[0]=y0

for i in range(1,n):

    k1=h*x[i-1]*y[i-1]**(1/3)

    k2=h*(x[i-1]+h)*(y[i-1]+k1)**(1/3)

    y[i]=y[i-1]+0.5*(k1+k2)

for i in range(n):

    print(x[i],y[i])

plt.plot(x,y,'o')

plt.xlabel('value of x')

plt.ylabel('value of y')

plt.title('Approximate Solution with RK-2 Method')

plt.show()

نتایج:

1.0    1.0

1.5    1.67926784096

2.0    2.80994158899

2.5    4.52558068947

3.0    6.96573342035

3.5    10.2725017487

پایتون: روش اویلر (Euler)

در مسائل مقدار اولیه، مقدار تابع در نقطه شروع داده می شود و با استفاده از روش های موجود مقدار آن را در سایر نقاط بدست می آوریم. در اینصورت منحنی تغییرات متغیر تابع بر حسب متغیر مستقل قابل رسم خواهد بود.

از جمله روش های حل مسائل مقدار اولیه می توان به روش های تیلور، اویلر و رانگ کاتا مرتبه دوم، سوم و چهارم اشاره نمود. در کلیه این روش ها مختصات هر نقطه با استفاده از مختصات نقطه ماقبلش بدست می آید. اساس کلیه این روش ها، استفاده از سری تیلور است.

تذکر: برای مطالعه توضیحات بیشتر به کتاب «کاربرد ریاضیات در مهندسی شیمی - روش های عددی» نوشته دکتر خراط مراجعه کنید.

روش اویلر:

در اینجا قصد دارم به بررسی یک مثال به روش اویلر بپردازم.

مثال:

معادله دیفرانسیل زیر را با استفاده از روش اویلر و برای حالت h = 0.5 حل کنید و مقدار تابع را تا x = 3.5 محاسبه کنید.

حل با استفاده از زبان برنامه نویسی پایتون (کدنویسی در محیط Spyder):

import numpy as np

from matplotlib import pyplot as plt

x0=1

y0=1

xf=3.5

n=6

h=(xf-x0)/(n-1)

x=np.linspace(x0,xf,n)

y=np.zeros([n])

y[0]=y0

for i in range(1,n):

    y[i]=y[i-1]+h*x[i-1]*y[i-1]**(1/3)

for i in range(n):

    print(x[i],y[i])

plt.plot(x,y,'o')

plt.xlabel('value of x')

plt.ylabel('value of y')

plt.title('Approximate Solution with Euler Method')

plt.show()

نتایج:

1.0   1.0

1.5   1.5

2.0   2.35853568191

2.5   3.6896463079

3.0   5.62119172863

3.5   8.28825954375

پایتون: انتگرال‌گیری عددی به روش ذوزنقه‌ای

در چند پست آتی قصد دارم که انتگرال‌گیری عددی به روش‌های مختلف را بررسی کنم. برای مطالعه توضیحات مربوط به این روش ها به کتاب کاربرد ریاضیات در مهندسی شیمی (دکتر خراط) مراجعه کنید. در این مطلب به کدنویسی انتگرال‌گیری عددی به روش ذوزنقه‌ای می پردازیم.

مثال:

# the function to be integrated

def func(x):

    return x**2

# define variables

a = 1.          # left boundary of area

b = 4.          # right boundary of area

dx = 1          # width of the trapezoids

# calculate the number of trapezoids

n = int((b - a) / dx)

# define the variable for area

Area = 0

# loop to calculate the area of each trapezoid and sum.

for i in range(1, n+1):

    #the x locations of the left and right side of each trapezpoid

    x0 = a+(i-1)*dx

    x1 = a+i*dx

    #the area of each trapezoid

    Ai = dx * (func(x0) + func(x1))/ 2.

    # cumulatively sum the areas

    Area = Area + Ai

#print out the result.

print ("Area = ", Area)

نتیجه:

Area = 21.5

یک نمونه کد دیگر برای انتگرال گیری عددی به روش ذوزنقه ای:

import numpy as np

x = np.linspace(1, 4, num=4)

y = x**2

I = np.trapz(y, x)

error = (I - 4)/4

print(I, error)

نتیجه:

I = 21.5

error = 4.375

پایتون: چندجمله‌ای‌های حداقل مربعات

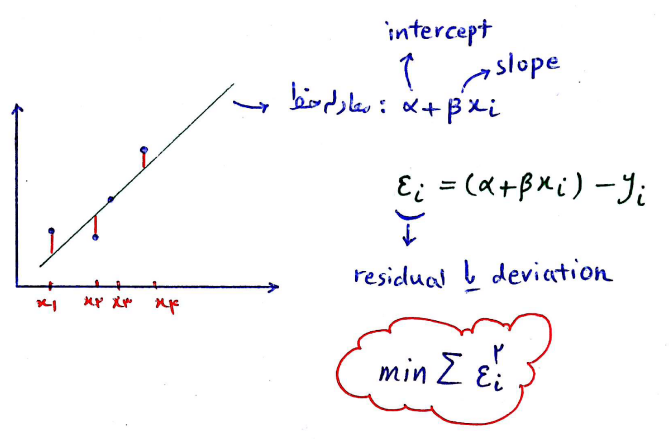
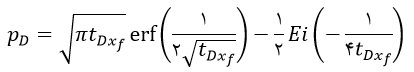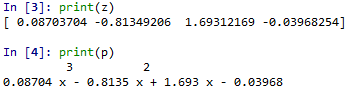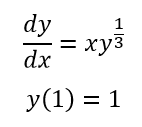برای مطالعه مبحث «چندجمله‌ای‌های حداقل مربعات» به کتاب «کاربرد ریاضیات در مهندسی شیمی - روش های عددی» که دکتر خراط نوشته اند مراجعه کنید. البته منابع مختلف دیگری هم در اینترنت موجود هست که به طور کامل توضیح داده اند. در کتاب دکتر خراط تمام روش های عددی و ریاضیاتی به طور مفصل و به همراه مثال توضیح داده شده اند که واقعا عالی هست.

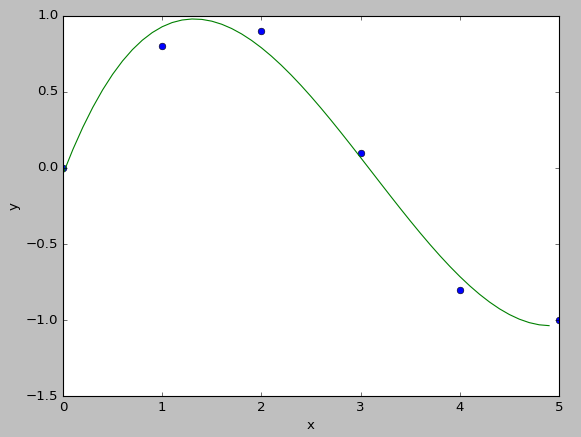
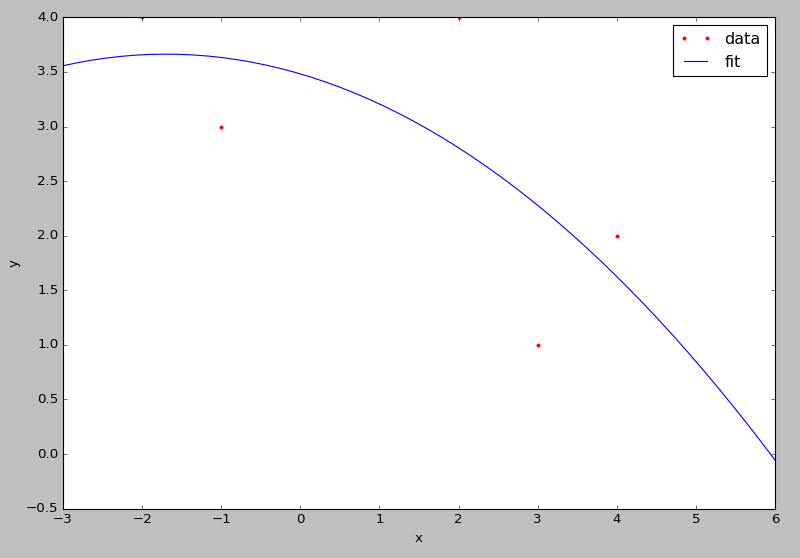
مثال: از پنج نقطه داده شده در زیر یک سهمی از روش حداقل مجموع مربعات خطا بدست آورید:

(-2,4) , (-1,3) , (2,4) , (3,1) , (4,2)

import numpy as np

import matplotlib.pyplot as plt

from scipy.optimize import curve_fit  # Use non-linear least squares to fit a function, f, to data.

xdata=np.array([-2,-1,2,3,4])  # fit this data with a function

ydata=np.array([4,3,4,1,2])

def func(x,p1,p2,p3):

    return p1*x**2+p2*x+p3   # I’d like to fit this function using nonlinear least squares.

popt,pcov=curve_fit(func,xdata,ydata,p0=(3,1,2))

print('parrameters=',popt)   # The variable popt contains the fit parameters

p1=popt[0]

p2=popt[1]

p3=popt[2]

residuals = func(xdata,p1,p2,p3)-ydata 

print('residuals=',residuals)

fres = sum(residuals**2)

print('fres=',fres)

xfit = np.linspace(-3,6)

yfit = func(xfit, popt[0], popt[1], popt[2])

plt.plot(xdata,ydata,'r.')

plt.plot(xfit,yfit,'b-') 

plt.show()

خروجی:

parrameters= [-0.06280788 -0.21305419  3.48275862]

residuals= [-0.34236453  0.63300493 -1.19458128  1.27832512 -0.37438424]

fres= 3.71921182266

منابع تکمیلی:

http://www.walkingrandomly.com/?p=5215

https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html