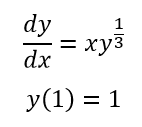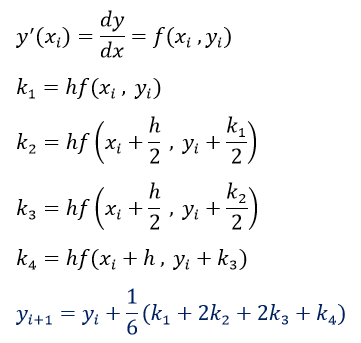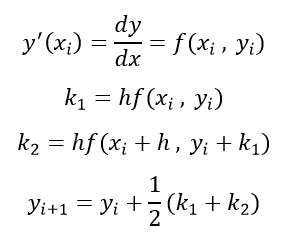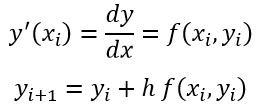در مسائل مقدار اولیه، مقدار تابع در نقطه شروع داده میشود و با استفاده از روشهای موجود مقدار آن را در سایر نقاط بدست میآوریم. در این صورت منحنی تغییرات متغیر تابع بر حسب متغیر مستقل قابل رسم خواهد بود.
از جمله روشهای حل مسائل مقدار اولیه میتوان به روشهای تیلور، اویلر و رانگ کاتا مرتبه دوم، سوم و چهارم اشاره نمود. در کلیه این روشها مختصات هر نقطه با استفاده از مختصات نقطه ماقبلش بدست میآید. اساس کلیه این روشها، استفاده از سری تیلور است.
تذکر: برای مطالعه توضیحات بیشتر به کتاب «کاربرد ریاضیات در مهندسی شیمی - روشهای عددی» نوشته دکتر خراط مراجعه کنید.
خلاصه روش رانگ کاتا مرتبه سوم:
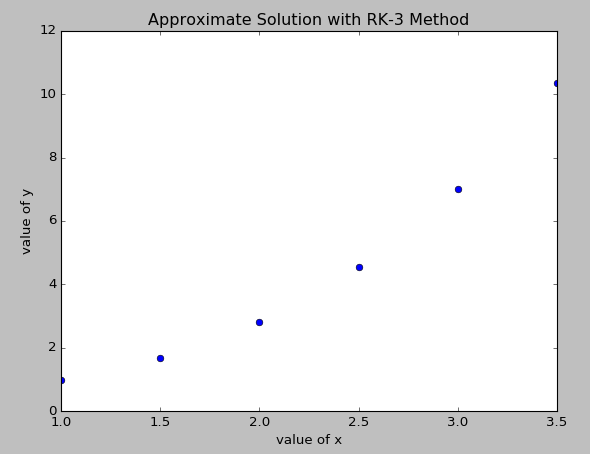
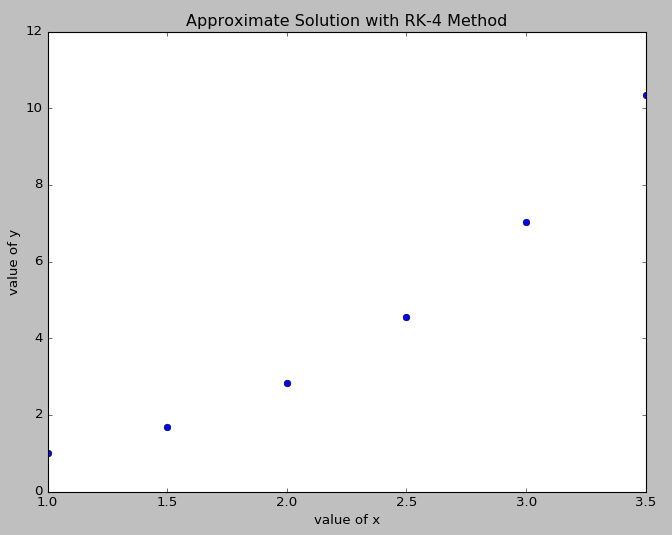
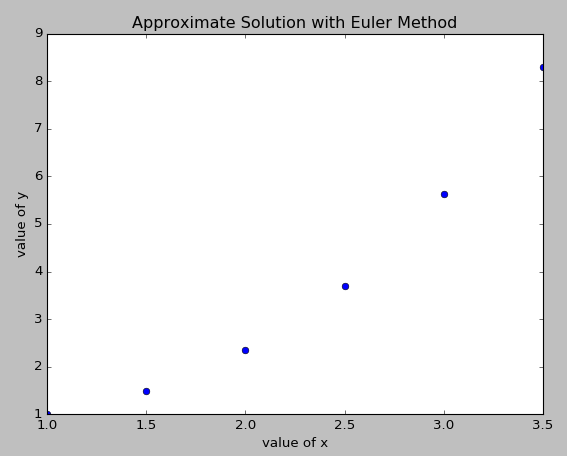
در اینجا قصد دارم به بررسی یک مثال به روش رانگ کاتا - 3 بپردازم. قبلاً این مثال را به روشهای اویلر، رانگ کاتا-2 و رانگ کاتا-4 نیز حل کردهام (+ و + و +)
مثال:
معادله دیفرانسیل زیر را با استفاده از روش رانگ کاتا مرتبه سوم و برای حالت h = 0.5 حل کنید و مقدار تابع را تا x = 3.5 محاسبه کنید.