چرا تا حالا دکترا نخوانده‌ام؟

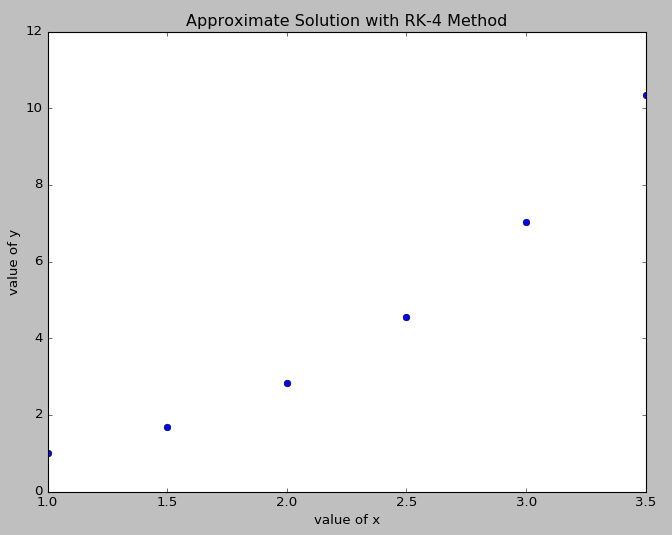
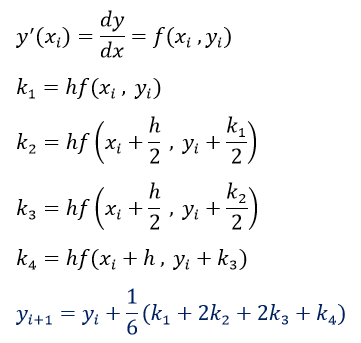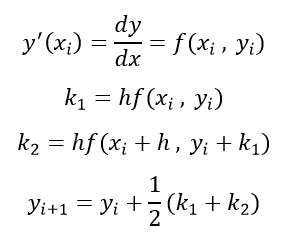الآن یکی از دوستان بهم ایمیل زده که چرا دکترا نخوندم؟

من نظر شخصیم رو میگم.

حدود یک سال و نیم فقط ولتست کار کردم. رفرنس ها رو خوندم، نرم افزارهاش رو تا حدودی یاد گرفتم و مقاله هم خوندم. ولی بعدش به این نتیجه رسیدم که این رشته سر دراز دارد. حالا حالاها میشه روش تمرکز کرد و ادامه داد. از یه جایی فهمیدم بقیه ماجرا رو باید در یک مقطع دیگه و با تمرکز ویژه ای ادامه داد که فعلا در حوصله من نیست.

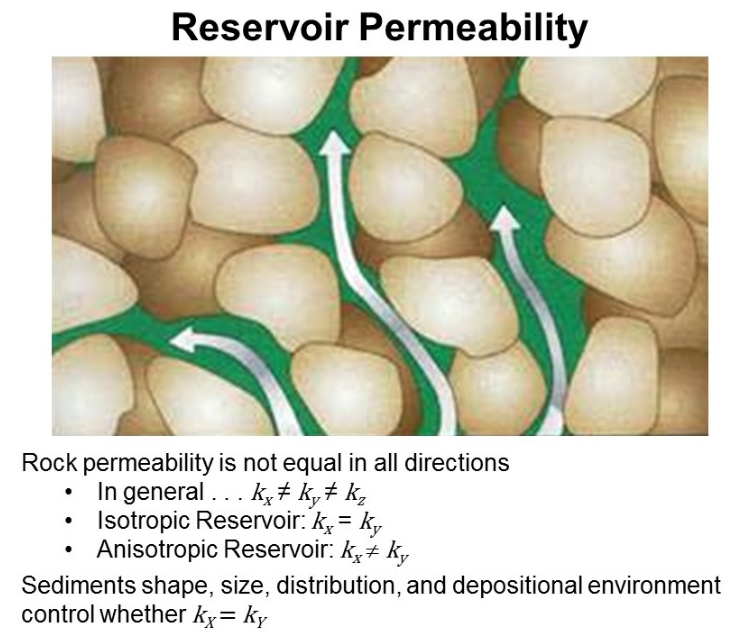
متوجه شدم که در ابتدا باید یک دید کلی از رشته مهندسی نفت بدست بیارم. باید مخزن رو بفهمم، چاه رو بفهمم، کوپل کردن این دوتا رو بلد باشم. باید بدونم وقتی میگن داریم فلان فرایند رو شبیه سازی میکنیم، دقیقا چه بلایی سر مخزن میاد. یعنی اول لازمه که به دیدگاه integrate در مهندسی نفت برسم. بتونم مباحث و عملیات نفت رو به هم ربط بدم. تا وقتی ندونم مبحث خواص سیال یعنی چه، چطوری میتونم از اون برای شبیه سازی و پیش بینی تولید استفاده کنم؟!! چطوری وقتی هنوز نمیدونم نقشه UGC زمین شناسی چی هست، میتونم آنالیز عددی در ولتست انجام بدم؟!!

حالا جدیدا فهمیدم که علاوه بر اینها، حتما حتما لازمه مفاهیم و مباحث "فاندامنتال" مهندسی نفت یعنی مکانیک سیالات، انتقال جرم و  حرارت و همچنین ریاضیات رو هم کاملا با پوست و گوشتم درک کنم. کسی به ما نبود بگه آقا اینا مهمن. این درسها باعث میشن که تفکر انتقادی پیدا کنی و به یک آدم متفکر تبدیل بشی که حرفی رو توی هوا نمیزنه و دقیقا برای تمام حرفاش دلیل و علت داره.

دو سال امریه بهترین فرصت برای این چیزهاست. 

چرا دروغ بگم؛ مدتیه از این شاخه به اون شاخه میپرم. نه اینکه سردرگم باشم، بلکه به این خاطره که پی بردم آدم باید مدتی رو اینطوری باشه تا دید خوبی از همه چی بدست بیاره.

اصن در حال حاضر پیشوند "مهندس" رو به "دکتر" ترجیح میدم. با مهندس بودن، آدم دستش خیلی بازتره. بیشتر علمی که الآن تو دکترا تولید میشه مثل یک کالای لوکس برای کشورمونه. ما کالای لوکس نیاز نداریم. ما اقتصاد بهتر و قوی تر میخوایم!

فکر میکنم دوره حالا، یه جورایی دوره "پیوند علوم مختلف به هم" هست. مثل همون دوره ابوعلی سینا و اینا. درسته یه عده دارن به صورت کاملا تخصصی مرزهای علم رو جلو میبرن، ولی شما باید تصمیم بگیرید توی کدوم گروه می خواهید باشید: گروهی که مرزها رو جابجا میکنن، یا گروهی که علم تولید شده توسط دیگران رو کاربردی و عملیاتی میکنن و در حقیقت اونو تبدیل به ارزش میکنن و بومی سازیش میکنن. من فعلا میخام جزو گروه دوم باشم و به همین خاطر نیازی به دکتر بودن هم ندارم. هرچند وجود هر دو گروه لازم و ضروری هست.

تو این دوره اگر بخواهیم جهش کنیم باید مباحث رشته های کامپیوتر و زمین شناسی و ریاضی و برق و ... رو هم وارد نفت کنیم. 

ممنون که خوندن این مطلب رو تحمل کردید.

صادق✋️

جزوه جدید درس چاه‌آزمایی (صادق سلمانی)

تا به حال خیلی از دوستان تقاضای قرار دادن جزوه چاه‌آزمایی نوشته شده توسط خودم را در سایت داشته‌اند ولی به دلیل اینکه ذهنم سمت کارهای دیگرم بوده فرصت نکردم در موردش تصمیم‌گیری کنم ولی امروز آن را برای دانلود در سایت قرار می‌دهم.

پیشنهاد اصلی من مطالعه کتاب‌های مرجع درسی هست و تمام مطالب این جزوه از همان کتاب‌ها گرفته شده‌اند ولی با ساختار منظم و طبقه‌بندی شده.

---

عنوان فایل: جزوه جدید درس چاه‌آزمایی

تهیه کننده: صادق سلمانی

مشخصات فایل: جزوه دست‌نویس و بسیار خوانا و خوش‌خط است.

حجم فایل: 63 مگابایت   

سال: آذر 96

تعداد صفحات: 130

کاربرد: دانشجویان مقطع کارشناسی و داوطلبان کنکور ارشد مهندسی نفت

 

دانلود چند صفحه از جزوه جهت مشاهده کیفیت آن

---

قیمت این محصول: 11500 تومان

 

بیشتر بخوانید: دانلود ویدئوهای آموزشی درس چاه‌آزمایی

آزمایش ضریب بهره‌دهی چاه «PI Test»

✅ برای انجام این تست مراحل زیر را باید داشته باشیم:

1) زمانیکه چاه در حال تولید است فشارسنج را پایین می‌بریم و فشارهای جریانی را ثبت می‌کنیم. این کار تا رسیدن گیج فشاری به عمق مورد نظر که به PI depth معروف است ادامه پیدا می‌کند. این عمق همان عمق گیج فشاری است و معمولاً 50 فوت بالاتر از مشبک‌ها قرار می‌گیرد. پس در این مرحله فشارهای جریانی چاه را بر حسب عمق ثبت می‌کنیم.

2) چاه را از سطح می‌بندیم و افزایش فشار درون چاه را ثبت می‌کنیم. افزایش فشار تا زمانیکه فشار چاه با فشار مخزن یکی شود ادامه پیدا می‌کند. پس در این مرحله داده های تست فشار استاتیک را در اختیار داریم.

3) برای تعیین دبی معمولاً اخرین دبی قبل از بسته شدن چاه را استفاده می‌کنند. این دبی با استفاده از رابطه تجربی گیلبرت و با داشتن پارامترهای لازم از جمله نسبت گاز به نفت تولیدی، اندازه قطر چوک، فشار جریانی سر چاه یا همان فشار قبل از ورود به چوک و ضرایب ثابت معادله گیلبرت، بدست می‌آید. این مقدار معمولاً با اختلاف 200 تا 300 بشکه کم یا زیاد بدست می‌آید. یک روش دیگر برای داشتن دبی، تعیین همه‌ی پارامترهای سنگ و سیال به طور دقیق و استفاده از رابطه دارسی است. 

4) با داشتن دبی و فشارهای جریانی و استاتیک میزان ضریب بهره‌دهی چاه مورد نظر بدست می‌آید. 

نکته: مدت زمان بسته بودن چاه بستگی به خصوصیات و شرایط مخزن دارد و ممکن است تا بیشتر از 100 ساعت هم طول بکشد.

پانوشت: نویسنده این مطلب آقای سروش جسری هستند.

مفهوم smoothing در نرم‌افزارهای چاه‌آزمایی

امروز یکی از دوستان سوالی در مورد smoothing پرسیده بودند. از آنجایی که من به همراه یکی از اساتیدم و همچنین یکی از مهندسان واحد بهره‌برداری شرکت مناطق نفت خیز جنوب در حال نوشتن یک کتاب در زمینه چاه‌آزمایی هستیم، به شخصه از سوالات دوستان استقبال می‌کنم. این باعث میشه که خودم هم به دنبال جواب بروم و در ویرایش کتاب هم کمک زیادی خواهد کرد.

✅ و اما منظور از smoothing چیست؟

یک مشکل عمده در تعیین و محاسبه مشتق فشار به روش بوردت، اختلالات و پراکندگی زیاد در مقادیر مشتق است. این مشکل زمانی بارزتر می‌شود که فاصله میان اندازه‌گیری‌های فشار خیلی کوتاه باشد. برای حل این مشکل به جای استفاده از همه نقاط برای محاسبه مشتق فقط از نقاطی با فاصله مشخص استفاده می‌شود. معمولاً مقدار x∆ کوچک است (0.01 تا 0.2) و در نرم‌افزارهای چاه‌آزمایی بیانگر smoothing می‌باشد. هرچه مقدار x∆ بزرگ‌تر باشد، مشتق فشار نیز smooth تر خواهد بود.

تذکر: دقت کنید که مثلا مقدار smoothing را برابر 1 نگذارید که این کار باعث میشه خطای زیادی بوجود بیاد. مقدار بهینه همان مقادیر 0.2 تا 0.3 است.

اگر هم علاقمند به مطالعه بیشتر در مورد روش محاسبه مشتق فشار هستید، لینک زیر را که مدتی پیش در سایتم نوشته‌ام مطالعه کنید:

نحوه محاسبه مشتق فشار برای رسم نمودارهای مشتق فشار در چاه آزمایی

کانال سایت در تلگرام

پایتون: روش رانگ کاتا مرتبه سوم (Runge-Kutta 3rd Order)

در مسائل مقدار اولیه، مقدار تابع در نقطه شروع داده می‌شود و با استفاده از روش‌های موجود مقدار آن را در سایر نقاط بدست می‌آوریم. در این صورت منحنی تغییرات متغیر تابع بر حسب متغیر مستقل قابل رسم خواهد بود.

از جمله روش‌های حل مسائل مقدار اولیه می‌توان به روش‌های تیلور، اویلر و رانگ کاتا مرتبه دوم، سوم و چهارم اشاره نمود. در کلیه این روش‌ها مختصات هر نقطه با استفاده از مختصات نقطه ماقبلش بدست می‌آید. اساس کلیه این روش‌ها، استفاده از سری تیلور است.

تذکر: برای مطالعه توضیحات بیشتر به کتاب «کاربرد ریاضیات در مهندسی شیمی - روش‌های عددی» نوشته دکتر خراط مراجعه کنید.

خلاصه روش رانگ کاتا مرتبه سوم:

در اینجا قصد دارم به بررسی یک مثال به روش رانگ کاتا - 3 بپردازم. قبلاً این مثال را به روش‌های اویلر، رانگ کاتا-2 و رانگ کاتا-4 نیز حل کرده‌ام (+ و + و +)

مثال:

معادله دیفرانسیل زیر را با استفاده از روش رانگ کاتا مرتبه سوم و برای حالت h = 0.5 حل کنید و مقدار تابع را تا x = 3.5 محاسبه کنید.

حل با استفاده از زبان برنامه نویسی پایتون (کدنویسی در محیط Spyder):

import numpy as np

from matplotlib import pyplot as plt

x0=1

y0=1

xf=3.5

n=6

h=(xf-x0)/(n-1)

x=np.linspace(x0,xf,n)

y=np.zeros([n])

y[0]=y0

for i in range(1,n):

    k1=h*x[i-1]*y[i-1]**(1/3)

    k2=h*(x[i-1]+0.5*h)*(y[i-1]+0.5*k1)**(1/3)

    k3=h*(x[i-1]+h)*(y[i-1]+2*k2-k1)**(1/3)

    y[i]=y[i-1]+(1/6)*(k1+4*k2+k3)

for i in range(n):

    print(x[i],y[i])

plt.plot(x,y,'o')

plt.xlabel('value of x')

plt.ylabel('value of y')

plt.title('Approximate Solution with RK-3 Method')

plt.show()

نتایج:

1.0                          1.0

1.5           1.6855277908

2.0            2.826623146

2.5           4.5570242827

3.0           7.0160178606

3.5           10.345325211

کانال سایت در تلگرام

پایتون: روش رانگ کاتا مرتبه چهارم (Runge-Kutta 4th Order)

در مسائل مقدار اولیه، مقدار تابع در نقطه شروع داده می‌شود و با استفاده از روش‌های موجود مقدار آن را در سایر نقاط بدست می‌آوریم. در این صورت منحنی تغییرات متغیر تابع بر حسب متغیر مستقل قابل رسم خواهد بود.

از جمله روش‌های حل مسائل مقدار اولیه می‌توان به روش‌های تیلور، اویلر و رانگ کاتا مرتبه دوم، سوم و چهارم اشاره نمود. در کلیه این روش‌ها مختصات هر نقطه با استفاده از مختصات نقطه ماقبلش بدست می‌آید. اساس کلیه این روش‌ها، استفاده از سری تیلور است.

تذکر: برای مطالعه توضیحات بیشتر به کتاب «کاربرد ریاضیات در مهندسی شیمی - روش‌های عددی» نوشته دکتر خراط مراجعه کنید.

خلاصه روش رانگ کاتا مرتبه چهارم:

در اینجا قصد دارم به بررسی یک مثال به روش رانگ کاتا - 4 بپردازم. قبلاً این مثال را به روش‌های اویلر و رانگ کاتا-2 نیز حل کرده‌ام (+ و +)

مثال:

معادله دیفرانسیل زیر را با استفاده از روش رانگ کاتا مرتبه چهارم و برای حالت h = 0.5 حل کنید و مقدار تابع را تا x = 3.5 محاسبه کنید.

حل با استفاده از زبان برنامه نویسی پایتون (کدنویسی در محیط Spyder):

import numpy as np

from matplotlib import pyplot as plt

x0=1

y0=1

xf=3.5

n=6

h=(xf-x0)/(n-1)

x=np.linspace(x0,xf,n)

y=np.zeros([n])

y[0]=y0

for i in range(1,n):

    k1=h*x[i-1]*y[i-1]**(1/3)

    k2=h*(x[i-1]+0.5*h)*(y[i-1]+0.5*k1)**(1/3)

    k3=h*(x[i-1]+0.5*h)*(y[i-1]+0.5*k2)**(1/3)

    k4=h*(x[i-1]+h)*(y[i-1]+k3)**(1/3)

    y[i]=y[i-1]+(1/6)*(k1+2*k2+2*k3+k4)

for i in range(n):

    print(x[i],y[i])

plt.plot(x,y,'o')

plt.xlabel('value of x')

plt.ylabel('value of y')

plt.title('Approximate Solution with RK-4 Method')

plt.show()

نتایج:

1.0      1.0

1.5       1.6860902679

2.0     2.82824535285

2.5     4.56006327111

3.0     7.02071665246

3.5     10.3518481736

پایتون: روش رانگ کاتا مرتبه دوم (Runge-Kutta 2nd Order)

در مسائل مقدار اولیه، مقدار تابع در نقطه شروع داده می شود و با استفاده از روش های موجود مقدار آن را در سایر نقاط بدست می آوریم. در اینصورت منحنی تغییرات متغیر تابع بر حسب متغیر مستقل قابل رسم خواهد بود.

از جمله روش های حل مسائل مقدار اولیه می توان به روش های تیلور، اویلر و رانگ کاتا مرتبه دوم، سوم و چهارم اشاره نمود. در کلیه این روش ها مختصات هر نقطه با استفاده از مختصات نقطه ماقبلش بدست می آید. اساس کلیه این روش ها، استفاده از سری تیلور است.

تذکر: برای مطالعه توضیحات در مورد روش رانگ کاتا-2 به کتاب «کاربرد ریاضیات در مهندسی شیمی - روش های عددی» نوشته دکتر خراط مراجعه کنید.

خلاصه این روش:

در اینجا قصد دارم به بررسی یک مثال به روش رانگ کاتا - 2 بپردازم. قبلاً این مثال را به روش اویلر نیز حل کرده ام (این پست).

مثال:

معادله دیفرانسیل زیر را با استفاده از روش رانگ کاتا مرتبه دوم و برای حالت h = 0.5 حل کنید و مقدار تابع را تا x = 3.5 محاسبه کنید.

حل با استفاده از زبان برنامه نویسی پایتون (کدنویسی در محیط Spyder):

import numpy as np

from matplotlib import pyplot as plt

x0=1

y0=1

xf=3.5

n=6

h=(xf-x0)/(n-1)

x=np.linspace(x0,xf,n)

y=np.zeros([n])

y[0]=y0

for i in range(1,n):

    k1=h*x[i-1]*y[i-1]**(1/3)

    k2=h*(x[i-1]+h)*(y[i-1]+k1)**(1/3)

    y[i]=y[i-1]+0.5*(k1+k2)

for i in range(n):

    print(x[i],y[i])

plt.plot(x,y,'o')

plt.xlabel('value of x')

plt.ylabel('value of y')

plt.title('Approximate Solution with RK-2 Method')

plt.show()

نتایج:

1.0    1.0

1.5    1.67926784096

2.0    2.80994158899

2.5    4.52558068947

3.0    6.96573342035

3.5    10.2725017487

یک نکته ساده در مورد معادلات دیفرانسیل با مشتفات جزئی

برای دیدن بقیه پست ها در مورد معادلات دیفرانسیل با مشتقات جزئی به این لینک مراجعه کنید.

تراوایی میانگین

توانایی محیط متخلخل برای عبور دادن سیال از میان خود را تراوایی (Permeability) می‌نامند و با نماد k نمایش می‌دهند. تراوایی یک محیط متخلخل به عواملی همچون تخلخل آن، شکل حفرات و میزان ارتباط حفرات به یکدیگر بستگی دارد.

تراوایی افقی: اگر یک چاه عمودی به صورت عمود بر یک مخزن افقی آن را قطع کند، تراوایی در جهت موازی با لایه‌ها اهمیت زیادی دارد.

تراوایی عمودی: تراوایی در جهت عمود بر لایه‌ها را تراوایی عمودی می‌نامند و در اثر نیروهای گراویته ایجاد می‌شود. این نوع از تراوایی در چاه‌های افقی طولانی اهمیت زیادی دارد.

روش های محاسبه تراوایی میانگین

برای محاسبه تراوایی میانگین، دانستن تاریخچه رسوب‌گذاری مخزن لازم است.

1- لایه‌ها موازی باشند: 

برای محاسبه تراوایی میانگین در مخازن لایه‌ای (layered reservoirs) از روش میانگین حسابی (arithmetic mean) استفاده می‌کنیم. رسوبات دلتایی، آبرفتی و رودخانه‌ای مثال‌های خوبی برای این مورد هستند.

2- لایه‌ها سری باشند:

برای محاسبه تراوایی میانگین یک مدل سری و خطی از روش میانگین هارمونیک (harmonic mean) استفاده می‌کنیم. به طور کلی، میانگین هارمونیک کمتر از میانگین حسابی است.

3- لایه‌ها به صورت رندوم توزیع شده باشند:

سنگ آهک و دولومیت تغییرات لیتولوژی سریع و رندومی را از خود نشان می‌دهند. زمانی که لایه‌ها به صورت رندوم و تصادفی توزیع شده باشند از روش میانگین هندسی (geometric averaging) استفاده می‌کنیم.

تذکر: اگر نفوذپذیری موثر که از طریق ولتست محاسبه می‌شود در دسترس باشد، باید آن را با تراوایی میانگین محاسبه شده بوسیله داده‌های مغزه مقایسه کرد.

حذف نقاط تاریک

هر چیزی رو که بلد نیستید و فکر میکنید یک روزی شما رو به دردسر خواهد انداخت، هرچه زودتر یاد بگیرید!