پس از سقوط قیمت نفت از سال 2014، پروژه‌های نفتی و همچنین سرمایه‌گذاری در این صنعت عظیم کاهش چشم‌گیری پیدا کرد. الآن بیش از هر زمان دیگری، سازمان‌ها باید از راه‌حل‌های فناوری اطلاعات و دیجیتالی‌سازی استفاده کنند.
✅ اگر علاقمند هستید که بدانید صنعت نفت و گاز دنیا در حال حرکت به چه سمتی است و چه تغییراتی در حال بوجود آمدن در آن است، حتما گزارش زیر را که مربوط به سال 2017 هست مطالعه کنید. 👇👇
✨به سوال زیر پاسخ بده و یکی از محصولات سایت را به دلخواه با تخفیف 40 درصد دریافت کن!✨
سوال:
✅ برای تفسیر داده‌های چاه‌آزمایی از نمودارهایی استفاده می‌شود که مقیاس‌های متفاوتی مانند کارتزین، نیمه‌لگاریتمی و یا لگاریتمی دارند.
🔰 حال سوال این است که دلیل استفاده از مقیاس نیمه‌لگاریتمی چیست؟ مگر این مقیاس چه ویژگی‌هایی دارد که ما را مجاب به استفاده از آن می‌کند؟
⏰ تا ساعت 20 روز پنج شنبه 9 شهریور پاسخ تشریحی و دقیق خود را تنها از طریق ایمیل ✉️ برای من ارسال کنید و بلافاصله کد تخفیف را به همراه پاسخ این سوال دریافت نمایید.
امیدوارم با این کار مطالعه دقیق‌تر و بهتری در زمینه چاه‌آزمایی داشته باشیم😊.
salmani.sgh@gmail.com
تابع خطا (Error Function) در ریاضیات، تابعی غیراصلی (نداشتن ضابطه صریح) است که در علوم احتمالات، مواد، آمار و معادلات دیفرانسیل با مشتقات جزئی استفاده می‌شود. تعریف این تابع به صورت زیر است (منبع: ویکی پدیا):
همچنین متمم تابع خطا (Complementary Error Function) نیز به شکل زیر تعریف می‌شود:
نمودار تابع خطا
جدول تابع خطا
علاوه بر اینها، در زبان برنامه‌نویسی پایتون نیز دستوری وجود دارد که می‌توان تابع خطای هر مقداری را محسابه نمود:
from math import *
erf (2)
>> 0.9953222650189527
سوالی که برخی اوقات پیش می‌آید این است:
چرا بعضی اوقات نمودار هورنر به صورت کاهشی است و برخی مواقع افزایشی؟
برای پاسخ به این سوال به توضیحات و شکل های زیر دقت کنید. سپس فایل ویدئویی را نیز با دقت مشاهده کنید. من توضیحات کامل را با یک سری داده در نرم‌افزار سفیر (لینک دانلود آموزش ویدئویی سفیر) و اکسل برای شما گفته‌ام.
مشاهده ویدئو در آپارات
پاسخ فشاری مخازن بسته در حالت‌های تولید، تزریق و بسته بودن چاه بسیار متفاوت است. در طول تست تولید یا تزریق، زمانی که موج فشار به آخرین مرز مخزن برسد، پروفایل فشار تثبیت شده و سپس به صورت یکنواخت به سمت پایین متمایل می‌شود. این قسمت از جریان، جریان شبه پایدار نامیده می‌شود و مشخصه آن وجود رابطه خطی بین افت فشار و زمان است:
آنالیز لگاریتمی:
الف) اگر مخزن در حال تولید یا تزریق باشد (تست کاهش فشار و یا تست تزریق)، به دلیل آنکه مرز مخزن بسته است یک جریان شبه پایدار (PSS) بوجود می‌آید و بنابراین شیب نمودار فشار و مشتق فشار در زمان‌های انتهایی برابر یک خواهد بود.
ب) برای زمانی که چاه بسته است (تست ساخت فشار)، فشار در مقداری برابر با فشار متوسط مخزن تثبیت می‌شود؛ بنابراین مقدار مشتق فشار به سمت صفر سقوط می‌کند؛ در حقیقت نمودار مشتق فشار به صورت نمایی به سمت پایین می‌رود.
اگر نمودار فشار ته چاهی بر حسب زمان در یک مختصات کارتزین رسم شود، رژیم جریانی PSS به صورت یک خط راست با شیب m می‌باشد که با استفاده از آن می‌توان سایز مخزن را محاسبه نمود.
در ویدئویی که در ادامه آورده شده است، من یک مثال کاربردی از مخازن بسته را در نرم‌افزار سفیر اجرا کرده‌ام و تمام مطالب ذکر شده در این پست را در ویدئو به طور کامل توضیح داده‌ام.
مدت زمان ویدئو: 12 دقیقه
حجم فایل: 35 مگابایت
قیمت: 4000 تومان
تذکر: پس از پرداخت وجه، تکمیل فرایند را بزنید و منتظر بمانید تا لینک دانلود در صفحه نمایشگر شما نشان داده شود.
اولین مرحله در مطالعه یک فرایند با شبیه‌سازی کامپیوتری، توسعه یک مدل برای سیستم واقعی است.
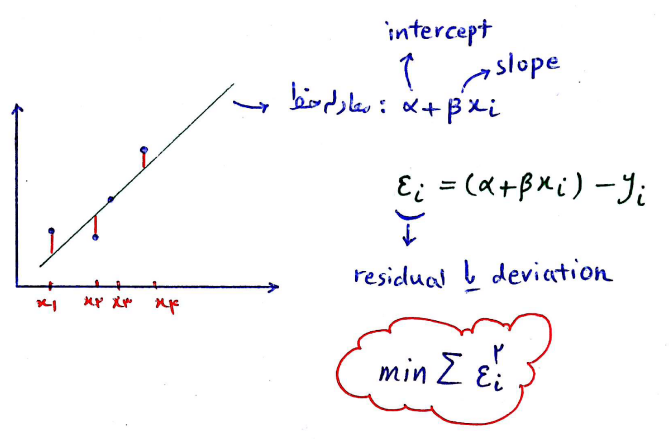
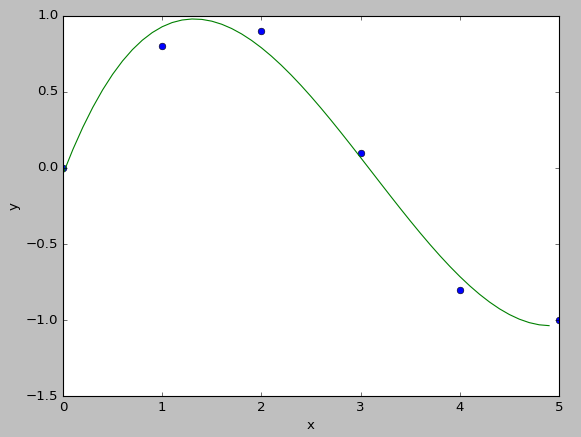
هنگام مطالعه حرکت یک شیء کوچک که تحت تأثیر نیروی گرانش زمین قرار دارد، ما ممکن است که بتوانیم نیروی اصطکاک هوا را نادیده بگیریم. در این حالت، مدل ما یک تقریبی از سیستم واقعی خواهد بود. معمولاً این مدل این اجازه را به ما خواهد داد تا رفتار سیستم (به فرم تقریبی) را از طریق معادلات ریاضی بیان کنیم، که اغلب شامل معادلات دیفرانسیل معمولی (ODE) یا معادلات دیفرانسیل با مشتقات جزئی (PDE) هستند.
در علوم طبیعی مانند فیزیک، شیمی و مهندسی، اغلب سخت نیست که یک مدل مناسب پیدا کنیم، اگرچه معادلات حاصل شده برای حل بسیار مشکل هستند و در اکثر موارد نمی‌توان آن‌ها را به طور تحلیلی حل نمود.
از سوی دیگر، در مواردی که نمی‌توان آن‌ها را به خوبی در چارچوب ریاضیات شرح داد و به رفتار اشیائی وابسته هستند که اقدام آن‌ها را نمی‌توان به طور قطعی پیش‌بینی نمود (مانند انسان‌ها)، یافتن یک مدل خوب برای توصیف واقعیت بسیار مشکل است. به عنوان یک قاعده کلی، در این رشته‌ها معادلات حاصله را ساده‌تر می‌توان حل نمود، اما یافتن آن‌ها سخت‌تر است و اعتبار یک مدل باید بیشتر مورد سوال قرار بگیرد. برخی از مثال‌های معمول عبارتند از تلاش برای شبیه‌سازی اقتصاد، استفاده از منابع طبیعی و غیره.
تا کنون، ما فقط در مورد توسعه مدل‌ها برای توصیف واقعیت بحث کرده‌ایم، و استفاده از این مدل‌ها لزوماً شامل کامپیوتر یا کار عددی نیست. در حقیقت، اگر معادله یک مدل بتواند به صورت تحلیلی حل شود، باید این کار را انجام داد و راه حل معادله را نوشت.
در عمل، تقریباً هیچ معادله مدل یک سیستم مورد نظر را نمی‌توان به صورت تحلیلی حل کرد، و این جایی است که کامپیوتر وارد می‌شود: با استفاده از روش‌های عددی، ما حداقل می‌توانیم مدل را برای یک مجموعه خاص از شرایط مرزی مطالعه کنیم.
به طور واضح مطلوب است که راه‌های تحلیلی را در هر کجا که امکان‌پذیر است پیدا کنید، اما تعداد مسائلی که این امکان وجود دارد کم هستند. معمولاً نتایج عددی یک شبیه‌سازی کامپیوتری بسیار مفید است (با وجود کاستی‌های نتایج عددی در مقایسه با روش تحلیلی)، زیرا این تنها راه ممکن برای مطالعه سیستم است.
نام مدلسازی کامپیوتری از دو مرحله برگرفته شده است: 1) مدلسازی؛ یعنی پیدا کردن توصیف مدل یک سیستم واقعی و 2) حل معادلات مربوط به مدل با استفاده از روش‌های محاسباتی، زیرا این تنها راه حل معادلات می‌باشد.
تعدادی زیادی پکیج وجود دارند که قابلیت‌های مدلسازی محاسباتی را ارائه می‌دهند. اگر اینها نیازهای تحقیق یا طراحی را برآورده کنند، و هرگونه پردازش و به تصویر کشیدن داده‌ها از طریق ابزارهای موجود پشتیبانی شود، می‌توان مطالعات مدلسازی محاسباتی را بدون هیچ گونه دانش برنامه‌نویسی عمیق‌تر انجام داد.
در یک محیط تحقیقاتی – هم در دانشگاه و هم در صنعت – اغلب به نقطه‌ای می‌رسند که پکیج‌های موجود قادر به انجام شبیه‌سازی مورد نظر نمی‌باشند. در این حالت، مهارت‌های برنامه‌نویسی مورد نیاز است.
درک نحوه ایجاد یک شبیه‌سازی کامپیوتری تقریباً به این صورت است: 1) یافتن مدل (اغلب به معنای یافتن معادلات درست می‌باشد)؛ 2) دانستن اینکه چگونه این معادلات را به صورت عددی حل کنیم؛ 3) پیاده‌سازی روش‌هایی برای محاسبه این راه حل‌ها (این برنامه‌نویسی است).
یکی از موضوعات مهم ریاضیات و آمار که کاربرد زیادی در رشته‌های مهندسی دارد، مبحث برازش منحنی (Curve Fitting) می‌باشد.
هدف ما در برازش منحنی آن است که بهترین خط یا منحنی ممکن را از داده‌های موجود عبور دهیم. برای آنکه متوجه شویم که بهترین چندجمله‌ای یا منحنی ممکن را انتخاب کرده‌ایم، باید مجموع مربعات باقمانده‌ها حداقل باشد:
.The most common choice is to minimize the sum of squared residuals
معرفی چند تابع:
1- z = polyfit (x, y, n)
این تابع، مقادیر x داده و مقادیر y داده‌ها را دریافت می‌کند و سپس یک منحنی درجه n ام از داده‌ها عبور می‌دهد به نحوی که بهترین انطباق ممکن را داشته باشد (حداقل مربعات).
2- p = poly1d (z)
یک تابع چند جمله‌ای از ضرایب می‌سازد.
بررسی یک مثال از مبحث برازش منحنی:
from numpy import *
x = array ([0.0 , 1.0 , 2.0 , 3.0 , 4.0 , 5.0])
y = array ([0.0 , 0.8 , 0.9 , 0.1 , -0.8 , -1.0])
z = polyfit (x, y, 3)
p = poly1d (z)
xs = [ 0.1 * i for i in range (50)]
ys = [p ( x ) for x in xs]
from pylab import *
plot (x, y, 'o', label='data')
plot (xs, ys, label='fitted curve')
ylabel ('y')
xlabel ('x')
show ()
🔸 بررسی انواع مرزها در نرم‌افزار سفیر
🔹 طراحی تست در نرم‌افزار سفیر (Test Design)
🔸 مخازن گازی در نرم‌افزار سفیر
🔹اثر جریان غیر دارسی در نرم‌افزار سفیر
🔸 گسل‌ها در نرم‌افزار سفیر
🔹چاه‌های افقی در نرم‌افزار سفیر
🔸چاه‌های دارای شکاف هیدرولیکی در نرم‌افزار سفیر
🔹تست تداخل و پالس در نرم‌افزار سفیر
🔸اثرات مربوط به چاه در نرم‌افزار سفیر
🔹مخازن چندلایه ای در نرم‌افزار سفیر
🔸 بررسی تست های ولتست کنکور ارشد و دکترای 96
✅ به مرور هر کدام از این موارد به صورت ویدئویی تدریس و ضبط خواهد شد و پکیج آموزش نرم افزار چاه آزمایی سفیر آپدیت می شود.
❗️دقت شود که آپدیت های جدید به صورت رایگان برای کسانی که قبلاً این محصول را خریداری کرده اند، ارسال می شود. ولی برای کسانی که جدیداً قصد تهیه آن را داشته باشند، با هر بار آپدیت، هزینه محصول بیشتر خواهد شد. در حال حاضر قیمت این فایل ویدئویی فقط 35000 تومان است و به تمام سوالات شما پاسخ خواهم داد.
لینک دانلود آموزش ویدئویی نرم‌افزار چاه‌آزمایی سفیر
لینک دانلود آموزش ویدئویی درس چاه‌آزمایی (ویژه مقاطع کارشناسی، کارشناسی ارشد و کنکور)
رابرت ارلافر (ROBERT CHARLES (“BOB”) EARLOUGHER JR.) در سال 1941 به دنیا آمد و در 18 آگوست 2011، در سن 70 سالگی درگذشت. او آرزو داشت که به عنوان یک مهندس و دانشمند به یاد آورده شود.
او مقاطع کارشناسی، کارشناسی ارشد و دکترای خود را در رشته مهندسی نفت تحصیل کرده است و هر سه مقطع را در دانشگاه استنفورد بوده است.
در سال 1966، او به عنوان مهندس تحقیق به شرکت نفت ماراتون (Marathon Oil Company) پیوست.
در سال 1977 مدیر بخش مهندسی شد.
او همواره سعی می کرد که نتیجه تحقیقات و پرژوهش ها را به صورت کاربردی در میادین نفتی به کار بندد.
او یک متخصص شناخته شده در زمینه تجزیه و تحلیل داده های چاه آزمایی بود و مقالات بسیاری در این زمینه و شبیه سازی مخزن و ازدیاد برداشت نفت به چاپ رسانیده است.
ارلافر در سال 1977 یک SPE monograph نوشت با نام Advances in Well Test Analysis (لینک دانلود کتاب) که 40000 نسخه فروخته است و هنوز نیز به عنوان یک مرجع درسی در برخی دانشگاه ها تدریس می شود.
او در سال 1979 جایزه Lester C. Uren را برای موفقیت متمایز در فن آوری مهندسی نفت و جایزه جان فرانکلین کارل در سال 1990 برای سهم برحسته او در استفاده از اصول مهندسی برای توسعه و بازیافت نفت کسب کرد.
در سال 1997، او به عنوان عضو افتخاری SPE نامگذاری شد، که بالاترین افتخاری است که SPE به یک فرد ارائه می دهد.
در کنفرانس سالانه SPE که در سال 2009 در New Orleans برگزار شد، او به عنوان "افسانه تولید و عملیات" (Legend of Production and Operations) شناخته شد.
علاقه اصلی ارلافر، هرچیزی در ارتباط با کوه های کلورودا بود. به طوری که در سال 2009 نوشت:
“wherever you place my remains, my heart remains in the Colorado mountains”
او همواره در این کوه ها، اسکی و کوهنوردی و پیاده روی می کرد.
او توسط همکاران و دوستان خود به خاطر عقل شگفت انگیزش، تعهدش به حرفه و شغلش و نگرانی اش برای دیگران، به یاد می‌آید.
منبع: https://www.nap.edu/read/18477/chapter/15
آیا تا به حال با خودتان فکر کرده‌اید که چرا در درس چاه‌آزمایی از مقیاس نیمه لگاریتمی و یا لگاریتمی استفاده می‌کنیم؟ مگر این مقیاس‌ها چه ویژگی‌ای دارند؟
📌 اغلب در چاه‌آزمایی از تعداد سیکل‌های لگاریتمی (log cycle) نام برده می‌شود. یک سیکل لگاریتمی معادل است با یک تغییر در مقدار بوسیله ضریبی از 10. برای مثال، فاصله از 1 تا 10، از 25 تا 250، و از 0.0137 تا 0.137 همگی طولی برابر با یک سیکل لگاریتمی دارند.
✅ در نمودارهای نیمه لگاریتمی و لگاریتمی، مقیاس محور زمان به صورت لگاریتمی می‌باشد و این باعث گسترش داده‌های اولیه می‌گردد. همان‌طور که در شکل زیر دیده می‌شود، داده‌های فشاری در بازه 10 تا 180 psi قرار گرفته‌اند. ولی حدود نیمی از داده‌های فشاری توسط محور y پوشانده شده‌اند. 👇👇
✅ این در حالی است که اگر مقیاس زمان به صورت لگاریتمی باشد، داده‌های اولیه گسترش می‌یابد و خواندن داده‌های فشاری در زمان‌های اولیه راحت‌تر می‌گردد. 👇👇
برای دنبال کردن مطالب چاه‌آزمایی در کانال تخصصی چاه‌آزمایی (https://t.me/WellTestTech) عضو شوید.
